按图15.3进行交易时的风险,只要注意到最大的损失就会清楚,风险为100%意味着一次的交易有全部损失的危险。在图15.3中最大亏损出现时,将使资产减少4%,建立这种25倍的仓,假如出现最大亏损时,就会全部损失掉。于是图15.3中的风险赌资率为4%。

图15.3 "可能情形数目“增多时的投资收益
这时,100次交易后资产的增长情形是,变成1.05倍在100次中有3次,变成1.04倍有6次……将这些相乘得到:
由此可以看出,100次交易后的资产将变成3.232倍,而每一次的资产的平均增长,只要将R开一百次方根就可以求出,即每一次的交易,其资产增长的期望值是1.18%。
其次,将风险的赌资率假设为它的2倍的8%。第一次交易张数也为风险4%时的倍数,也就是说,资产达1.10倍时的概率为4%,达1.08倍时的概率为6%……这时若想求出交易100次之后的资产的增长,应该是:
每一次的交易按期望值的2.32%增加资产。如此地继续计算下去的结果见表15—3,每交易一次,最高的资产增长是在风险赌资率为82%~83%时的15.22%(表15—3以4为一个刻度来表示,所以为80%的下一个赌资率是84%)。从中可见,即使规则完全相同,只要风险的赌资率不同,资产的增长就会完全不同。
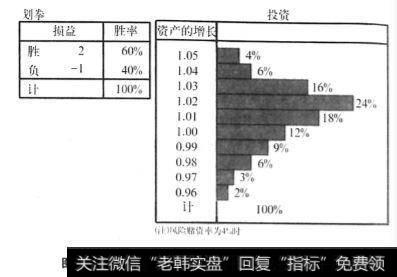
表15—3 风险赌资率与资产增长
要点
是否获利取决于赌资率的选择。











