交易员所面临的最严重的问题之一就是有可能发生灾难性的亏损。灾难性的亏损是指超过交易员预算的亏损,它远大于交易所需的投资资金或者保证金。曾经发生过一笔糟糕的交易在金融领域而毁灭一个交易员这样的事情。毫无疑问,悲剧还会上演。
针对灾难性风险,有两种普遍的看法。第一种看法认为交易员实际上承受痛苦的概率很小,甚至几乎不值得考虑这些风险;第二种看法认为,一个人会损失其大半财富的这种可能性足以警戒所有人,除了那些有勇无谋的鲁莽者。
两种看法都有可取之处。很显然,每个交易员和潜在的交易员都应该仔细思考承担灾难性亏损的可能性。同时,那些发现自己很难接受这样的可能性的人应该避免冒险。
灾难性风险是指交易员除了损失交易资金之外所要承担的风险。显而易见,如果交易员将所有资产投入交易,他没有承担任何灾难性风险,许多年轻的交易员都是这么做的。如果交易员有130000美元资产,而将其中的100000美元投入交易,他就不必过多地担心灾难性亏损。如果交易员蒙受了500000美元的亏损,他就破产了,但是破产和一系列亏损交易没有多大区别。这种方法对大多数交易员来讲都不是审慎的方法,尤其是那些年老的交易员,或者企业交易者。
对大多数交易员而言,一个更有用的途径是保护一部分资产以防被扣押。我知道投资者有多种方式来保护资产。例如,将资金放入合格的养老计划中就很安全,直到退休。将资金放入短期信托中就很安全,直到资金回流到创造者手里。在亏损前将资金转给其他的家庭成员很安全,但是资金就不再是给予者的了。
或者,由一个全资公司进行交易,而不是由交易员来进行交易。通过限制股东或者公司官员的欺诈,公司的股东仅对投入资本和他们作出的保证负责。当然,交易员可能已经是某个养老计划或者保本基金的法人,他不想冒险投入所有资金,这样一来,公司就能分拆一个全资子公司。由于法律比市场还要多变,交易员应该在通过法律途径保护资金前咨询律师。
如果交易员不能保护大部分的资产,他就应该花上半个小时左右的时间想象一旦亏损是自己能冒险资金量的十倍,会发生什么。他感觉如何?他的妻子感觉如何?他的孩子和邻居感觉如何?如果他是一个公司的职员,他的老板或者董事会将感觉如何?这些人会怎么做?他对这些人的感觉会作何感想?他不得不采取哪些行动?
毫无疑问,灾难性亏损相当可怕。对许多人而言,没有潜在的利润值得冒险。对另一些人而言,如果承担灾难性亏损的概率足够小交易值得冒险。这是一个重要的前提条件。许多交易员断然不会接受这样的风险。的确,许多交易员阅读本章是因为他们不想要这些风险。但是这并不能完全消除风险。必须有人承担这些风险。许多时候,这不是慈善行为甚至是愚蠢的行为。更多时候,承担风险的个人或者公司会因此得到回报。考虑到大多数投资者是多么强烈地想要避免风险,承担风险的投资者很可能回报颇丰。
只有报酬相对大于风险时,才值得卖给其他交易员类似灾难性亏损保险的产品。但是风险有多大呢?
经济学家曾经认为他们确切了解任何价格变化的可能性。那时,经济学家相信股票和商品价格变化呈正态分布。如果价格变化事实上是正态分布,知道分布的平均数和标准差,那么我们就能知道该分布的所有信息。
的确,如果价格变化实际上呈正态分布,超过距平均数三个标准差的价格变化出现的概率应小于0.01;而超过十个标准差的价格变化应该几乎不会发生。如果价格变化呈正态分布,灾难性风险就不会是个严重的问题。
不幸的是,灾难性风险是一个严重的问题。
当曼德布罗特宜布某些投机价格不是正态分布时,经济学家们都很震惊。这些分布看上去是正态分布,而且,有强有力的数学原因能证明为什么这些分布应该是正态分布。尽管如此,曼德布罗特还是坚持它们不是正态分布。曼德布罗特注意到,分布的尾部比在正态分布情况下要更密集,因此,事实上分布不呈正态分布。
曼德布罗特相信正确的分布是一个稳定帕累托分布。这一论断没有得到很多赞同。我们已经彻底研究了正态分布的数学运算,但却不了解稳定帕累托分布的数学运算。
的确,我们只真正了解三种特殊情况的分布:掷硬币、正态分布和柯西分布(我们稍后讨论)。这些例子实际上都相对简单。的确,所有这三种分布都能通过两个变量来完全描述,例如平均数和标准差。
另一方面,稳定帕累托分布需要四个变量才能描述一个分布:位置、尺度、斜度和峰度。位置是分布的居中趋势,可以由平均数或者中位数测量。尺度是分布的宽度或者分散度,可以由标准差或者绝对偏差均值测量。斜度是分布的对称性(如图9-1),峰度是分布尾部的密集度(如图9-2)。
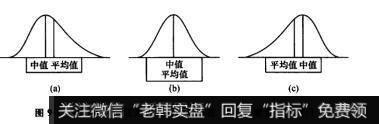
图9-1斜度可以是正向的(a)、不存在(b)或者负向的(c)
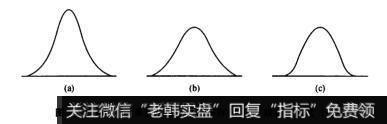
图9-2峰度可以呈尖峰状(a)、不存在(b)或者平顶状(c)
该分布最重要的变量就是峰度。分布的峰度决定了使用哪种统计工具来测量其他的三个变量。一个稳定帕累托分布的峰度(X)由一个介于0至2的量表来测量,不包括0,包括2。当分布呈对称,且X等于2时,该分布就呈正态分布。当分布是正态分布时,平均数就是位置的有效测量,标准差就是分散度的有效测量。
然而,当X小于2,标准差很快就变得没有意义了。所幸只要X大于1,绝对偏差均值就是分散度的有效测量;而不幸的是,只要X大于1,绝对偏差均值和平均数就是唯一有效的测量量。当X等于1且分布是对称时,该分布就是柯西分布。当分布是柯西分布时,或者更一般地讲X小于等于1时,理性交易就变得相当困难了(如图9-3)。
问题是没有真正理想的、有用的有效测量能够确定类似柯西分布的分布位置。最理想的测量量就是算术平均数,即平均数。但是当X小于等于1时,平均数不是一个有效的测量量。这意味着一个过去可获利的交易方法无法保证持续带来利润。样本容量为十亿与样本容量为1一样有用,也一样没用。
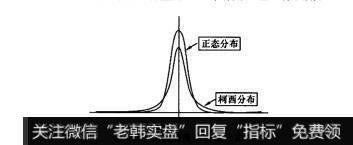
图9-3正确的商品价格分布
解图:正确的商品价格分布似乎处于正态分布和柯西分布之间,如果我们能忽略斜度。但学生t分布,稳定帕累托分布的分布,以及其他分布和家族分布都包括这一范围。
我们仍然能够测量位置。例如,中位数仍然可以有效测量类似柯西分布的分布。它没有真正告诉交易员想知道的事情,当我们无法获知平均数时,仅能知道中位数,然而,中位数并非理想的测量量。
所幸价格看上去不是一个柯西分布,至少我所知道的已发表的价格行为研究文献中没有这样的例子。不幸的是,X的估值在样本与样本之间差异极大,所以我们很难准确地说X是什么,尽管它似乎介于1和2之间(见表9-1)。
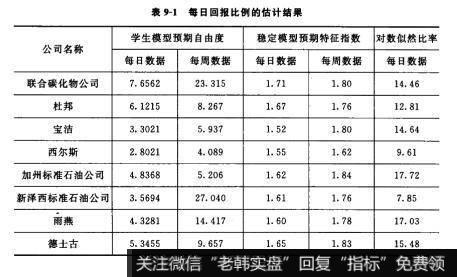
表9-1每日回报比例的估计结果
有趣的是,稳定帕累托分布并非只能描述从正态分布到柯西分布的分布,学生分布也能描述,而且我们更了解学生分布。
换句话说,在某种程度上灾难性亏损是可以规避的。
我们既有战略又有策略来消除灾难性风险,或者将其最小化。战略方法不包括预测,策略方法包括预测。我们先来讨论战略方法。











