欧式期权的拥有者只能在期满日当天执行期权,所以其各种定价方法相对较为简单。本次探讨如何估计欧式期权的价格以及与之相关的标的物价格是如何变动的。
探讨的方法是:
首先,假设投资者是风险中性的,并且在期满日,股票价值两个极限之间任何股票价格出现的概率是均等的。在这种情况下,为期权估值是很容易的,也可以对期权定价的基础和期权价格相关于其标的物价格变动的特性有一个直观感受。其次,设定厌恶风险的投资者进入市场,但是假定在到期日标的物只有两种可能的价格,即期权必须定价,这样可以利用它来形成一种无风险投资策略,获得投资的无风险收益。最后,进一步作出更符合实际的假设,即假定股票的收益率是正态分布的,按照布莱克-斯科尔斯期权定价模型原理估计期权的价值。
二项式期权定价:
假定投资者的投资为风险中性,再放宽这个假设,讨论构成无风险有价证券组合产生无风险收益的期权如何定价。假设在到期前可以划分任意多个时期,随着时期数目的增加,最后一个时期期末最终股票价格的概率分布接近于正态分布,如果期权风险和风险补偿对证券价格有影响,期权风险在有价证券定价中起重要作用,那么,厌恶风险的投资者运用资本资产定价模型对期权定价就可能不合适。
1973年,布莱克和斯科尔斯发表了一篇论文,这篇论文解开了这个谜。用与他们所说的股票相联系的期权,可以用来构成无风险投资。作为一个案例,当投资者构造一种无风险的有价证券组合的时候,这些期权必须以一定的价格售出,这样投资者将在有价证券组合投资中获得无风险收益。
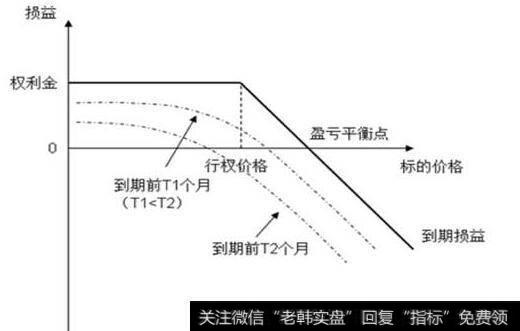
看跌期权价格和基础股票价格之间的关系为一种单调减曲线。如果股票的价格为27.27美元(执行价格的现值),曲线的切线斜率为-0.5,这意味着,如果股票价格上升1.00美元,则看跌期权的价格将下降近0.50美元。投资者可以通过购买某种股票的1份和2份看跌期权,构成一个无风险的有价证券组合。在这种情况下,看跌期权的价格下降可由股票价格的上升完全抵消。
当然,伴随着股票价格的每一变化,投资者就移动到了该关系曲线上的一个新点上,该点则有新的切线斜率,所以投资者必须根据持有的股票份额,适当调整与其相联系的看跌期权的份数。在任何情况下,通过调整投资者的有价证券组合,投资者可以随时保持其无风险状态。如果有价证券组合是无风险的,那么它将产生与其他无风险投资一样的收益率。这样,看跌期权将以形成这种情况的一种价格出售。











