无监督的自组织映射(Self-Organizing Map, SOM)网络具有高度并行处理机制、高度容错能力,是解决聚类问题的强有力工具.在解决聚类问题方面表现出很好的优越性。与其他聚类方法相比,SOM网络的优点在于:可以实现自学习,网络具有自稳定性,无须外界给出评价函数,能够识别向量空间中最有意义的特征,抗噪音能力强等,因此该模型在模式识别、机器控制、语音识别、图像压缩、向量量化及组合优化等方面具有广泛的应用。
本案例在具有智能背景的SOM神经网络的基础上,利用改进的SOM模型对股票进行分析。
SOM神经网络
SOM神经网络的拓扑结构由两层节点构成:输入层和输出层(竞争层),其结构如图11-3所示。图中上层为输出层,输出层中的节点是以二维形式排成的一个节点矩阵,它们中的每个节点是一个输入向量的代表。输入层处于下方,若输入节点为个,则输入向量为维,输入层节点与输出层中的所有节点通过权值实现全互连。
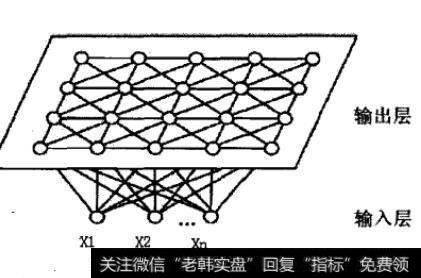
图11-3 SOM网络结构
输出层节点之间实行侧抑制连接,它与节点之间的权值分布有关,在获胜节点邻域区域内的节点相互激励,邻域区域可以是正方形,也可以是六角形。它是关于时间的函数,随着时间的增加,邻域的面积成比例缩小。区域以外的节点相互抑制,而更远的又有较弱的激励作用,通常用Bubble(墨西哥帽)函数来表示神经元之间的这种侧反馈作用。
应用这种侧反馈原理,使每个获胜神经元附近形成一个聚类区。由于聚类区内的各神经元的权重向量保持与输入向量逼近的趋势,从而使具有相近特征的输入向量聚集在一起。
Kohonen分别定义了SOM神经网络的邻域函数α(t)、学习速率因子函数n (t),如公式(1)、公式((2)所示。
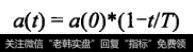 (1)
(1)
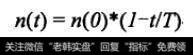 (2)
(2)
式中:t为迭代次数,T为预设的最大迭代次数。α(0), n(0)为初始时刻的邻域半径和学习速率因子,α(0)在学习的初始时刻覆盖范围较大,随着时间的增加,a(0)逐渐减小,n(t)值的选取范围通常为[0,1]。
另外,Kohonen还定义了获胜节点及其邻域内节点的连接权修正公式,如公式(3)、(4)所示。
 (3)
(3)
 (4)
(4)
式中:Wij(t+1)为t+l时刻输入节点i与输出节点j之间的连接权,N*j(t)为t时刻以获胜节点为中心的邻域范围。
对于Kohonen提出的SOM模型,每次进行连接权修正后,各输出神经元对应于输入模式空间的最邻近区域都在不断地变化,不同的输入模式对应着不同的变化,因此使网络最终的收敛结果与输入顺序有关。但如果选取一个较小的学习速率因子,并且学习速率因子和邻域半径都在一个合适的函数关系范围内变化,则对于输入顺序的敏感性将会得到改善或避免。鉴于上述因素,本案例在SOM的基础上,改进了网络中的邻域函数如公式(5)所示,学习速率因子函数如公式(6)所示。
 (5)
(5)
 (6)
(6)











